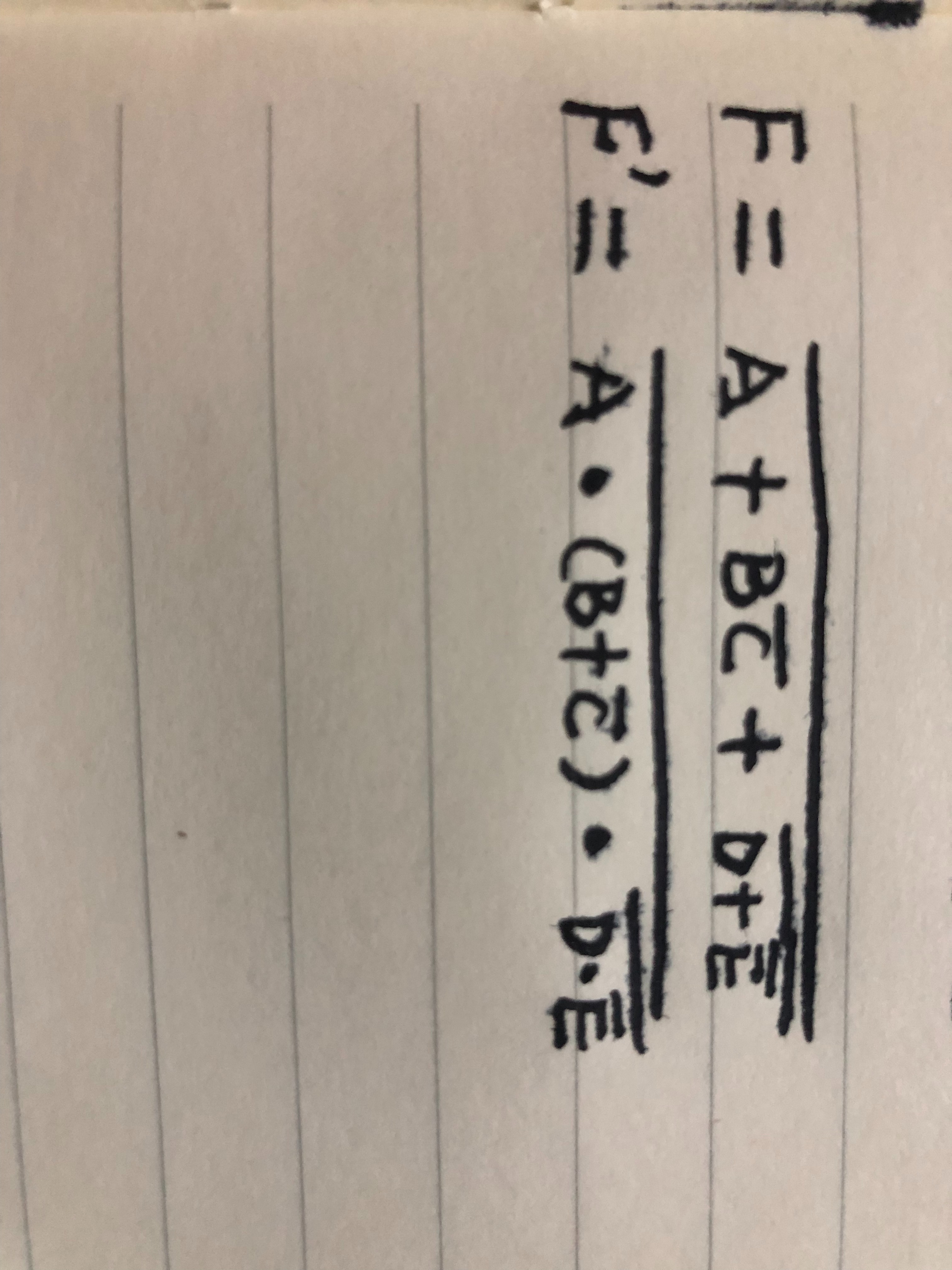基本公式

常量和常量

1. 0 * 0 = 0
2. 0 * 1 = 0
3. 1 * 1 = 1
4. 1 + 1 = 1
5. 1 + 0 = 1
6. 0 + 0 = 0
7. 0' = 1
8. 1' = 0

注：与运算是乘法，或运算是加法，0 为假，1 为真。

常量和变量

1. A * 1 = A
2. A * 0 = 0
3. A + 1 = 1
4. A + 0 = A

变量和变量

1. A * A = A
2. A + A = A
3. A * A' = 0
4. A + A' = 1
5. (A')' = A

交换律

1. A * B = B * A
2. A + B = B + A

结合律

1. (A * B) * C = A * (B * C)
2. (A + B) + C = A + (B + C)

分配律

1. A * (B + C) = A * B + A * C
2. A + (B * C) = (A + B) * (A + C)

反演律（摩根定理）

1. (A * B)' = A' + B'
2. (A + B)' = A' * B'
3. 反演律实现了与和或的变化

注：重点

异或运算

1. A 异或 B = B 异或 A
2. 异或也有交换律和结合律，例：(A 异或 B) 异或 C = A 异或 (B 异或 C)

因果互换律

若 A 异或 B 等于 C，则有 A 异或 C 等于 B，B 异或 C 等于 A

定理

优先级从大到小依次是：括号、非、与、或

代入定理

可以把上面的公式带到一个式子里进行运算。

反演规则

在一个逻辑式中，若将其中

• 所有 “ + ” 变为 “ * ”
• 所有 “ * ” 变为 “ + ”，同时加括号。
• 所有 0 变为 1
• 所有 1 变为 0
• 所有原变量变为反变量
• 所有反变量变为原变量

所得到的逻辑式即为原逻辑式的反逻辑式。

注：若一个逆运算不属于单个变量时，原样输出。

对偶规则

在一个逻辑式中，若将其中

• 所有 “ + ” 变为 “ * ”
• 所有 “ * ” 变为 “ + ”，同时加括号。
• 所有 0 变为 1
• 所有 1 变为 0

所得到的逻辑式即为原逻辑式的对偶式。

注：若一个逆运算不属于单个变量时，原样输出。

若两个逻辑式的对偶式相等，则两个逻辑式也是相等的。